Loss Landscape: Heavy Tail Self-regression (HT-SR)

这是一篇关于 Traditional and Heavy-Tailed Self Regularization in Neural Network Models 的笔记.

Setup

设 $W \in \mathbb{R}^{N \times M}$ 是一个随机矩阵, $N$ 是样本数, $M$ 是权重的维度.

Marchenko-Pastur (MP) theory

Marchenko-Pastur (MP) 理论是一个用于描述随机矩阵的谱分布的理论.

Marchenko-Pastur (MP) theory
$W$ 的经验谱分布 $\rho_{W}(\lambda)$ 可以由以下公式给出:

$\rho_{N}(\lambda) \xrightarrow[Q \text{ fixed}]{N \rightarrow \infty} \begin{cases} \displaystyle \frac{Q}{2 \pi \sigma_{mp}^{2}} \frac{\sqrt{(\lambda^{+} - \lambda) (\lambda - \lambda^{-})}}{\lambda}, & \text{if } \lambda \in [\lambda^{-}, \lambda^{+}] \\ 0, & \text{otherwise}\end{cases}$

其中, $\lambda^{\pm} = (1 \pm \frac{1}{\sqrt{Q}})^{2}$, $\sigma_{mp}^{2} = 1$, $Q = \frac{N}{M} \geq 1$.

最大特征值 $\lambda_{max}$ 的分布 $\rho_{\infty}(\lambda_{max})$ 由 Tracy-Widom 定律控制.

Heavy-Tailed extensions of MP theory

MP 理论是基于高斯假设的, 但在实际应用中, 权重矩阵中的元素存在强相关性, 且不满足高斯假设, 反而更接近于重尾分布.
最近的研究表明，对于某些重尾分布，MP理论存在新的普适类(Universality class)。
我们假设 $W$ 的元素服从独立同分布的重尾分布, 且满足以下条件:

Heavy-Tailed
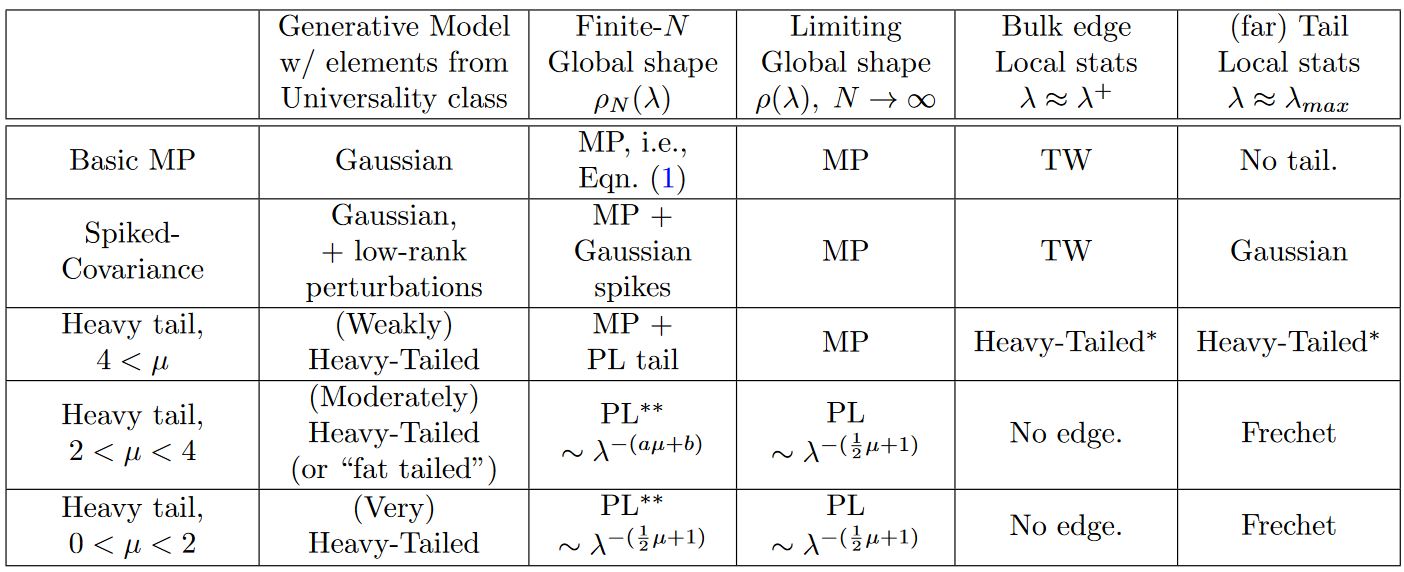
对于服从 $W_{ij} \sim P(x)=\frac{1}{x^{1+\mu}},\ \mu \gt 0$ 的权重矩阵 $W$, MP 理论存在以下三种新的普适类:

弱重尾 ($4 \lt \mu$)
中重尾 ($2 \lt \mu \lt 4$)
强重尾 ($0 \lt \mu \lt 2$)

通过拟合幂律分布的指数 $\alpha$, 可以判断出对应的μ值, 从而确定矩阵属于哪一个重尾普适类.

Empirical results

小模型
对于较老和较小的DNN模型 (如LeNet5和一个小型的MLP3模型), 其权重矩阵的ESD表现出弱自正则化特征，可以用MP理论的扰动变体”尖峰协方差模型”很好地建模. 在这种情况下, 少数特征值从随机矩阵本体中拉出, 导致MP软秩和稳定秩都降低. 这种弱自正则化类似于Tikhonov正则化, 因为存在一个”尺度”将”信号”与”噪声”清晰分离, 但又不同于显式的Tikhonov正则化, 因为它是DNN训练过程本身隐式导致的。
大模型
对于现代的大型DNN模型 (包括AlexNet、Inception等), 其权重矩阵的ESD与基于高斯分布的标准MP模型有很大偏离, 它们反而似乎属于重尾随机矩阵模型的某个普适类, 即”重尾自正则化”. ESD呈现重尾特征，但有有限支撑. 在这种情况下，即使在理论上也没有一个”尺度”能清晰地将”信号”与”噪声”分离.