Stochastic Process: 马尔可夫链

马尔可夫链

马尔可夫链
给定随机变量序列 $\{ X_{n}, n=1,2,\cdots \}$, 如果对 $1 \leq n_{1} < n_{2} < \cdots < n_{k}$, 及 $i_{1}, i_{2}, \cdots, i_{k} \in E$, 有

$P \{ X_(n_{k+1}) = i_{k+1} \vert X_{n_{1}} = i_{1}, X_{n_{2}} = i_{2}, \cdots, X_{n_{k}} = i_{k} \} = P \{ X_{n_{k+1}} = i_{k+1} \vert X_{n_{k}} = i_{k} \}$

则称 $\{ X_{n}, n=1,2,\cdots \}$ 为马尔可夫链. 称 $E = \{ 1, 2, \cdots, m \}$ 为状态空间.

转移概率
设 $\{ X_{n}, n=1,2,\cdots \}$ 为马尔可夫链, 称

$p_{i, j}(n, k) = P \{ X_{n+k} = j \vert X_{n} = i \}$

为 $\{ X_{n}, n=1,2,\cdots \}$ 在时刻 $n$ 的 $k$ 步转移概率, 称

$P(n, k) = \left( p_{i, j}(n, k) \right) \quad (i,j \in E)$

为 $\{ X_{n}, n=1,2,\cdots \}$ 在时刻 $n$ 的 $k$ 步转移概率矩阵.
特别地, 当 $k=1$ 时, 称 $p_{i, j}(n, 1) = p_{i, j}(n)$ 为 $\{ X_{n} \}$ 在时刻 $n$ 的转移概率, 称 $P(n) = \left( p_{i, j}(n) \right)$ 为 $\{ X_{n} \}$ 在时刻 $n$ 的一步转移概率矩阵.

若随机变量序列 $\{ X_{n}, n=1,2,\cdots \}$ 为独立增量过程, 且 $X(0)=0$, 则 $X_{n}$ 为马尔可夫链.

离散参数齐次马氏链

离散参数齐次马氏链
设 $\{ X_{n}, n=1,2,\cdots \}$ 为马尔可夫链, 如果其一步转移概率 $p_{i, j}(n,1)$ 恒与起始时刻 $n$ 无关, 记为 $p_{ij}$, 则称 $\{ X_{n}, n=1,2,\cdots \}$ 为离散参数齐次马氏链.

若随机变量序列 $\{ X_{n}, n=1,2,\cdots \}$ 为平稳独立增量过程, 且 $X(0)=0$, 则 $X_{n}$ 为齐次马尔可夫链.

初始分布 & 绝对分布
称 $p_i = P(X(0)=i), i \in E$, 为马氏链 $\{ X(n) \}$ 的初始分布, 记为 $\mathbf{\tilde{P}}_{0}$.
称 $p_j(n) = P(X(n)=j), j \in E$, 为马氏链 $\{ X(n) \}$ 的绝对分布, 记为 $\mathbf{\tilde{P}}_{n}$.

性质:

C-K 方程: $p_{i,j} (k+l) = \sum_{r \in E} p_{i,r}(k) p_{r,j}(l)$
平稳性: $P(n) = P^{n}$
绝对分布由初始分布和转移概率确定, 且满足 $\mathbf{\tilde{P}}_{n} = \mathbf{\tilde{P}}_{0} P^n$
齐次马氏链的有限维分布由初始分布和转移概率确定, 且满足 $P \{ X(n_{1}) = i_{1}, \cdots X(n_{k}) = i_{k} \} = \sum_{i \in E} p_{i} \cdot p_{i,i_{1}} \cdots p_{i_{k-1},i_{k}}$

离散齐次马氏链的状态分类

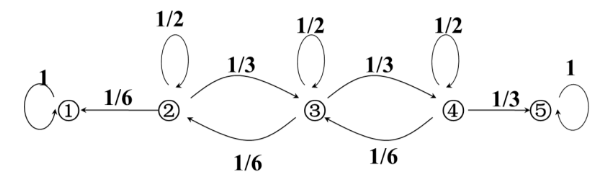
状态转移概率图形:

可达 & 互通

可达
设 $i,j \in E$, 若 $\exists n \geq 1$, 使 $p_{i,j}(n) \gt 0$, 则称状态 $i$ 可达状态 $j$, 记为 $i \rightarrow j$.
互通
若 $i \rightarrow j$ 且 $j \rightarrow i$, 这称状态 $i$ 与状态 $j$ 互通, 记为 $i \leftrightarrow j$.

首达时刻 & 首达概率 & 常返状态 & 周期

首达时刻
从状态 $i$ 出发，首次到达状态 $j$ 的时刻 $T_{ij}$ 称为首达时刻.
首达概率
从状态 $i$ 出发, 经过 $n$ 步首次到达状态 $j$ 的概率为 $f_{ij} = P \{ T_{ij}=n \vert X(m)=i \}$ 称为首达概率.
常返状态
设 $i \in E$, 若 $f_{ii}=1$, 则称状态 $i$ 为常反状态; 否则, 称为非常返状态.
周期
记 $d(i)$ 为满足 $p_{ij}(n) \gt 0$ 的所有 $n$ 的最大公约数. 若 $d(i) \gt 1$, 称 $i$ 有周期 $d(i)$, 否则称 $i$ 为非周期的。

闭集 & 吸收状态 & 可约集

闭集
设 $C$ 是 $E$ 的一个子集, 如果 $\forall i \in C, \forall j \not \in C, \forall n \geq 0$, 有 $p_{ij}^{(n)} = 0$, 则称 $C$ 是闭集.
吸收状态
设 $i \in E$, 如果状态子集 $\{ i \}$ 是闭集, 则称状态 $i$ 为吸收状态.
可约集
设是闭集, 如果 $C$ 中不再含有任何非空真闭子集, 则称 $C$ 是不可约闭集; 如果状态空间 $E$ 是不是约的，那么该马尔可夫链是不可约的, 否则称为可约的.

性质:

$p_{ij}(n) = \sum_{m = 1}^{n} f_{ij} p_{jj}(n-m)$
$f_{ij} \gt 0 \Leftrightarrow i \to j$
$i$ 是常反状态 $\Leftrightarrow$ $\displaystyle\sum_{n=1}^{\infty} p_{ii}(n) = \infty$; $i$ 是非常反状态 $\Leftrightarrow$ $\displaystyle \sum_{n=1}^{\infty} p_{ii}(n) = +\infty$
若 $i \leftrightarrow j$, 则 $i$ 与 $j$ 同为常反状态或同为非常反状态, 若它们均为常返态, 则它们同为正常返态或零常返态.、
齐次马尔科夫链的状态空间 $S$ 可唯一地分解成有限或可列无限多个互不相交的状态子集之并, 即 $S = D \cup C_{1} \cup C_{2} \cup \cdots$, 其中 $D$ 是吸收状态集, $C_{1}, C_{2}, \cdots$ 是不可约闭集.

离散参数齐次马氏链的遍历性

遍历态
离散参数齐次马氏链 $\{ X_{n}, n=1,2,\cdots \}$ 若状态 $i$ 为正常返且为非周期, 则称 $i$ 为遍历态。

离散参数齐次马氏链的平稳分布
离散参数齐次马氏链 $\{ X_{n}, n=1,2,\cdots \}$ 若存在 $\{ v_{j}, j \in E \}$, 满足条件:

$v_{j} \geq 0, j \in E$
$\displaystyle \sum_{j \in E} v_{j} = 1$
$\displaystyle v_{j} = \sum_{i \in E} v_{i} p_{ij}$

则称 $\{ X_{n} \}$ 是平稳的, $\{ v_{j}, j \in E \}$ 为离散参数齐次马氏链 $\{ X_{n} \}$ 的平稳分布.

极限分布
若离散参数齐次马氏链 $\{ X_{n}, n=1,2,\cdots \}$ 的绝对分布存在, 即 $\lim_{n \to \infty} \pi_{j}(n) = \pi_{j}^{} \ (j \in S)$ 存在, 则称 $\pi^{} = \{ \pi_{0}, \pi_{1}, \cdots \}$ 为 $\{ X_{n} \}$ 的极限分布.